如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB、AC于点E、G.连接GF.下列结论:①∠AGD=112.5°;②AD=2AE;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确结论的序号是 ,并说明理由.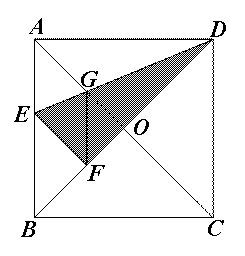
答案
①④⑤
解:①∵折叠正方形纸片ABCD,使AD落在BD上
∴∠1=∠2=![]() ∠ADB=22.5°
∠ADB=22.5°
又∵∠GAD=45°
∴∠AGD=180°-∠1-∠3=180°-22.5°-45°=112.5°
∴①正确
②∵折叠正方形纸片ABCD,使AD落在BD上
∴AE=EF,∠EFB=90°
又∵∠4=45°
∴在Rt△BEF中,利用勾股定理:![]()
∴![]()
∵AD=AB
∴![]()
∴②错误
③∵折叠正方形纸片ABCD,使AD落在BD上
∴S△AGD=S△FGD>S△OGD
∴③错误
④∵折叠正方形纸片ABCD,使AD落在BD上
∴AE=EF,AG=GF,∠7=∠8
∵∠5=∠6=45°
∴AG∥EF
∴∠8=∠9
∴∠7=∠9
∴AE=AG
∴AG=EF
∴四边形AEFG是平行四边形
又∵AE=EF
∴四边形AEFG是菱形
∴④正确
⑤由④的结论知:四边形AEFG是菱形
∴AE∥GF
∴∠OGF=∠5=45°
∵∠AOB=90°
∴由勾股定理得:![]()
∵![]()
∴![]()
∴⑤正确
综上:①④⑤为正确选项
知识点:四边形折叠
略
略








