如图，四边形ABCD为一梯形纸片，AB∥CD，AD=BC．翻折纸片ABCD，使点A与点C重合，折痕为EF．已知CE⊥AB．（1）求证：EF∥BD；（2）若AB=7，CD=3，求线段BC，BD的长．
答案
（1）如图1:
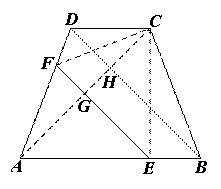图1
连接AC，分别交EF、BD于点G、H，则由轴对称性质，得AC⊥EF，AE=CE，∠AEG=∠CEG
∵CE⊥AB
∴∠AEG=∠CEG=45°，∠EAC=∠ACE=45°
∵在梯形ABCD中，AD=BC
∴∠DAB=∠CBA
又AB=BA
∴△DAB≌△CBA（SAS）
∴∠DBA=∠CAB=45°
∴∠DBA=∠AEG
∴EF∥BD.
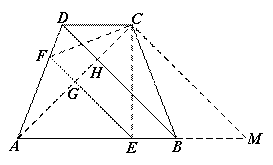（2）如图2:
图2
过点C作CM∥BD∥EF，交AB的延长线于点M，则四边形DBMC为平行四边形，
∴BM=CD=3，∠ACM=∠AHB=90°，CM=DB=AC
∴△ACM为等腰直角三角形
∴BD=CM=
又CE⊥AB
∴AE=ME=5，
∴CE=5，BE=2
∴BC=
知识点：四边形折叠
略
略
WORD格式（
