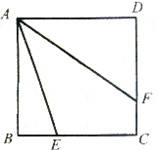
如图，已知正方形ABCD中，E为BC边上任意一点，AF平分∠DAE．求证：AE－BE＝DF．
答案
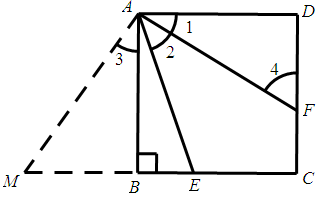
证明：延长CB到M使BM=DF，连结AM .在△ADF和△ABM中
∴△ADF≌△ABM（SAS）∴∠1=∠3，∠M=∠4，由于AB∥DC，AF平分∠EAD，所以∠BAF=∠4，∠1=∠2，∴∠2=∠3，从而∠MAE=∠BAF=∠4=∠M，∴AE=ME=BM+BE=DF+BE，∴AE-BE=DF .
知识点：全等三角形的判定与性质 等腰三角形的性质 正方形的性质
本问题的关键是将DF转移到与AE，BE都有关的位置，运用等量代换解题。首先补短，将DF移到BE处，来证明AE=BM+BE .而解决AE=BM+BE 问题的关键是角度的转换。∠BAF=∠4是关键。
将DF进行合理的转化
WORD格式（
