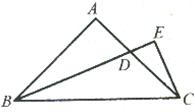
如图,已知△ABC中,∠A=90º,AB=AC,BE平分∠ABC,CE⊥BD于E,求证:CE= BD.
BD.
答案
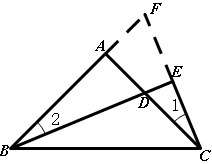
延长CE交BA的延长线于点H,由BE平分ABC,BE
CE,得CE=EH=
CH。
又 1+
H=90°,,
2+
H=90°
1=
2
在△ACH和△ABD中
HAC=
DAB=90°
AC=AB
1=
2
△ACH≌△ABD(ASA)
CH=BD
CE=
CH=
BD
知识点:全等三角形的判定与性质 直角三角形的性质
根据题意,要证明CE=BD,延长CE与BA,由题意的垂直平分线可得CE的两倍长CH,只需证明CH=BD即可,很显然有全等可以证明出结论
不能正确利用题中已知条件BF平分∠ABC,CE⊥BD于E,做出辅助线,进而解答。








