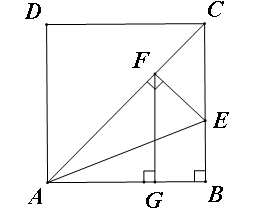
教材6题：如图所示．已知：在正方形ABCD中，∠BAC的平分线交BC于E，作EF⊥AC于F，作FG⊥AB于G．求证：AB²=2FG²．

答案

证明：∵∠BAC的平分线交BC于E
∴∠CAE=∠BAE，又∵EF⊥AC，FG⊥AB
∴EF=EB
在Rt△AEF和Rt△AEB中，
EF=EB
AE=AE
∴AB=AF
在Rt△AGF中，利用勾股定理得：AG²+FG²=AF²
并且△AGF是等腰直角三角形，即AG= FG
∴AB²=2FG²

知识点：全等三角形的判定与性质  勾股定理  正方形的性质  

证明：∵∠BAC的平分线交BC于E
∴∠CAE=∠BAE，又∵EF⊥AC，FG⊥AB
∴EF=EB
在Rt△AEF和Rt△AEB中，
EF=EB
AE=AE
∴AB=AF
在Rt△AGF中，利用勾股定理得：AG²+FG²=AF²
并且△AGF是等腰直角三角形，即AG= FG
∴AB²=2FG²

不会进行线段之间的转换

下载次数：5

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>