如图，已知四边形ABCD中，AD∥BC，若∠DAB的平分线AE交CD于E，连结BE，且BE恰好平分∠ABC，判断AB的长与AD＋BC的大小关系并证明.

答案

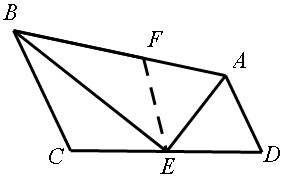
在BA上截取BF=BC，
∵BE恰好平分 $\footnotesize \angle$ ABC
∴ $\footnotesize \angle$ CBE= $\footnotesize \angle$ FBE
又BC=BF，BE=BE
∴△BCE≌△BFE
∴ $\footnotesize \angle$ C= $\footnotesize \angle$ BFE
又AD∥BC ∴ $\footnotesize \angle$ C+ $\footnotesize \angle$ D=180°
而 $\footnotesize \angle$ BFE+ $\footnotesize \angle$ AFE=180°
∴ $\footnotesize \angle$ AFE= $\footnotesize \angle$ D
又∵AE=AE， $\footnotesize \angle$ EAF= $\footnotesize \angle$ EAD
∴△AEF≌△AED
∴AF=AD
∴AD+BC=AF+BF=AB

知识点：三角形的角平分线、中线和高全等三角形的判定与性质

要证明两条线段和等于一条线段，最常想到的是截长补短法.
截长：在BA上截取BF=BC或者在AB上截取AF=AD；
补短：延长BC至G，使BG=BA

不会利用截长补短方法解题

下载次数：2

WORD格式（含答案版下载无答案版下载）

<<上一题下一题>>