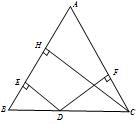
已知等腰△ABC中, AB=AC,CH是腰AB上的高,D是BC上任意一点,过D点做DE⊥AB,DF⊥AC,求证:DE+DF=CH
答案
过点C作CG⊥ED,交ED的延长线于点G,则四边形HEGC为矩形
∴HC=EG,AB∥CG
∴B=
DCG
∵AB=AC ∴B=
FCD
∴FCD=
GCD
又CD=CD,DFC=
DGC=90°
∴△CDF≌△CDG
∴DF=DG
∴DE+DF=DE+DG=EG=CH
知识点:全等三角形的判定与性质 等腰三角形的性质 直角三角形的性质
可通过截长补短的方法来证明
没有思路








