求证直角三角形斜边上的中线等于斜边的一半.

答案

如图，在Rt△ABC中，=90°，CD为AB边上的中线.求证：CD=AB.

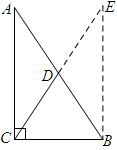
证明：延长CD至点E，使DE=CD，连结BE.
 在△ACD和△BED中，∵ED=CD，ADC=BDE，AD=BD  
∴△ADC≌△BDE ∴AC=BE，ACD=E
∴AC∥BE   ∴CBE=90°  =ACB
又BC=BC，AC=BE  ∴△ABC≌△ECB
∴AB=CE=2CD 即得证.

通过补短的方法来做，可延长CD至E，使DE=CD，然后证明AB=CE即可.

没有思路

下载次数：5

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>