△ABC中，∠BAC=60°，∠C=40°，AP平分∠BAC交BC于P，BQ平分∠ABC交AC于Q，求证：AB+BP=BQ+AQ．

答案

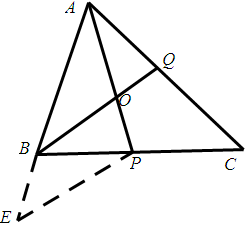
延长AB到E使BE=BP，连接EP，则AE=AB+BE=AB+BP，∠ABC=180°-∠BAC-∠C=80⁰.
由BQ平分∠ABC，AP平分∠BAC，则∠BAP=∠PAC=30°，∠ABQ=∠CBQ=40°.
又因为∠C=40⁰，我们得到CQ=BQ，BQ+AQ=CQ+AQ=AC。
$\because$    BE=BP， $\angle$ ABP=80°
$\therefore$ ∠E= $\frac{1}{2}$ $\times$ 80°=40°=∠C
在△APE和△APC中
   ∠E=∠C
    ∠BAP=∠CAP=30°
    AP=AP
$\therefore$    △APE≌△APC（AAS）
$\therefore$ AE=AP
即AB+BP=BQ+AQ

知识点：三角形的角平分线、中线和高三角形内角和定理全等三角形的判定与性质

见答案详解

正确作出辅助线，根据等量代换，把没有联系的线段转化为符合题目要求的线段。

下载次数：2

WORD格式（含答案版下载无答案版下载）

<<上一题下一题>>