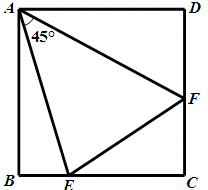
在正方形ABCD中，E、F分别是BC、CD上的点，且∠EAF=45°，求证：EF=BE+FD.

答案

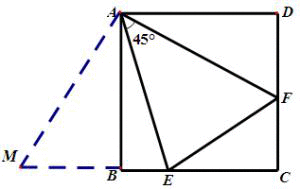
延长EB到M使BM=DF，连接AM。在三角形FAD和三角形MBA中
    $\angle$ D= $\angle$ ABM=90⁰
     DF=BM
     AD=AB
$\therefore$ 三角形FDA $\stackrel{\backsim}{=}$ 三角形MBA（SAS）
$\angle$ DAF= $\angle$ BAM，AF=AM。
又 $\angle$ EAF=45⁰
$\therefore$ $\angle$ BAE+ $\angle$ DAF=45⁰
$\therefore$ $\angle$ BAE+ $\angle$ BAM= $\angle$ MAE=45⁰= $\angle$ FAE

在三角形MAE和三角形FAE中
   MA=FA
   $\angle$ BAM= $\angle$ FAE
   AE=AE
$\therefore$ 三角形MAE $\stackrel{\backsim}{=}$ 三角形FAE(SAS)
$\therefore$ EF=EM=BE+BM=BE+FD.

知识点：全等三角形的判定与性质正方形的性质

见答案

做辅助线是一个难点，需要多多练习。

下载次数：2

WORD格式（含答案版下载无答案版下载）

<<上一题下一题>>