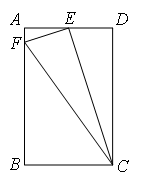
已知：如图，在矩形ABCD中，E为AD的中点，EF⊥EC交AB于F，连接FC（AB＞AE）.△AEF与△EFC是否相似，若相似，证明你的结论；若不相似，请说明理由.
答案
解：（1）△AEF∽△ECF.证明如下：延长FE与CD的延长线交于G，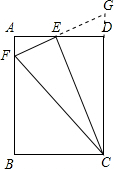
∵E为AD的中点，AE=DE，∠AEF=∠GED，
∴Rt△AEF≌Rt△DEG.∴EF=EG.
∵CE=CE，∠FEC=∠CEG=90°，
∴Rt△EFC≌Rt△EGC
∴∠AFE=∠EGC=∠EFC.
又∵∠A=∠FEC=90°，
∴Rt△AEF∽Rt△ECF.
知识点：相似三角形的判定与性质
利用倍长的思想，来倒角，证明两三角形相似
略
WORD格式（
