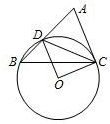
已知：如图，在△ABC中，D是AB边上一点，⊙O过D、B、C三点，∠DOC＝2∠ACD＝90°．
（1）求证：直线AC是⊙O的切线；
（2）如果∠ACB＝75°，⊙O的半径为2，求BD的长．

答案

（1）∵OD=OC，∠DOC=90°，
∴∠ODC=∠OCD=45°．
∵∠DOC=2∠ACD=90°，
∴∠ACD=45°．
∴∠ACD+∠OCD=∠OCA=90°．
∵点C在圆O上，
∴直线AC是圆O的切线．
（2）2

知识点：切线的判定与性质  

（1）证明OC⊥AC即可．根据∠DOC是等腰直角三角形可得∠DCO=45°．又∠ACD=45°，所以∠ACO=90°，得证；
（2）∵OD=OC=2，∠DOC=90°，
∴CD=．
∵∠ACB=75°，∠ACD=45°，
∴∠BCD=30°，
作DE⊥BC于点E，则∠DEC=90°，

∴DE=DCsin30°= ．
∵∠B=45°，
∴DB=2．

略

下载次数：4

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>