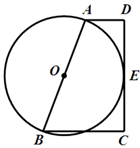
如图，已知梯形ABCD中，AD∥BC，DC⊥BC，AB=AD+BC，且AB为的直径．
求证：与DC相切．

答案

作OE⊥CD交CD于点E，所以OE∥AD∥BC，AO=BO，则DE=CE，所以OE是梯形的中位线，所以OE=（AD+BC），因为AB=AD+BC，则AB=2OE，则OE是半径，则由切线定理的推论可得与DC相切

知识点：切线的判定与性质  

作垂直，证是半径。
作OE⊥CD交CD于点E，所以OE∥AD∥BC，AO=BO，则DE=CE，所以OE是梯形的中位线，所以OE=（AD+BC），因为AB=AD+BC，则AB=2OE，则OE是半径，则由切线定理的推论可得与DC相切

略

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>