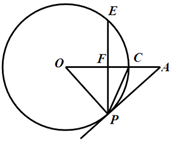
如图，A是外一点，连OA交于C，过上一点P作OA的垂线交OA于F，交于E，连结PA，若∠FPC=∠CPA．
求证：PA是的切线．

答案

EP⊥OA，∠FPC+∠FCP=90°，OC=OP，∠OCP=∠OPC，因为∠FPC=∠CPA，则有∠OPC+∠CPA=∠OCP+∠FPC=90°，则OP⊥AP，过圆上一点且垂直于直径的直线是圆的切线，所以PA是的切线

知识点：切线的判定与性质  

作半径，证垂直。
EP⊥OA，∠FPC+∠FCP=90°，OC=OP，∠OCP=∠OPC，因为∠FPC=∠CPA，则有∠OPC+∠CPA=∠OCP+∠FPC=90°，则OP⊥AP，过圆上一点且垂直于直径的直线是圆的切线，所以PA是的切线

不会灵活应用切线定理及其推论

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>