如图已知∠ADC＝∠ABC，BE，DF分别平分∠ABC.∠ADC，且∠1=∠2，求证：∠A=∠C.

证明：∵BE，DF分别平分∠ABC，∠ADC（已知）
∴∠1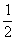＝∠ABC，∠3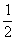＝∠ADC（）
∵∠ABC＝∠ADC（已知）
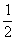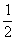∴∠ABC＝∠ADC（等式的性质）
∴∠1＝∠3（）∵∠1＝∠2（已知）
∴∠2＝∠3（）
∴（）∥（）（内错角相等，两直线平行）
∴∠A＋∠ADC＝180°，∠C＋∠ABC＝180°（）
∴∠A＝∠C（等式的性质）
①角平分线的性质②AB∥CD③AD∥BC④DF∥BE⑤角平分线的定义⑥等式的性质⑦等量代换⑧两直线平行，同旁内角互补⑨同旁内角互补，两直线平行

• A.①⑥⑦②⑧
• B.⑤⑥⑦③⑨
• C.①⑦⑦②⑧
• D.⑤⑦⑦④⑧

答案

正确答案：C

知识点：同位角、内错角、同旁内角  

略

略

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>