如图，已知BD为△ABC的角平分线，且BD=BC，E为BD延长线上一点，BE=BA，过点E作EF⊥AB于点F，则下列结论：
①△EBC可由△ABD绕点B旋转而得到；②∠BCE+∠BCD=180°；
③∠ABE=∠DAE；④BA+BC=2BF；则正确的结论有(    )个

①∵BD为△ABC的角平分线，
∴∠ABD=∠CBD，
在△ABD和△EBC中，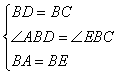
，
∴△ABD≌△EBC（SAS），
∴△EBC可由△ABD绕点B旋转而得到，
故①正确；
②∵△ABD≌△EBC，
∴∠BCE=∠BDA，
∴∠BCE+∠BCD=∠BDA+∠BDC=180°，
故②正确；
③∵BD=BC，BE=BA，∠ABE=∠CBE，
∴∠BEA=∠BCD=∠BDC=∠BAE，
∴∠AED=∠ADE=∠BCD=∠BDC，
∴∠CBD=∠DAE，
∴∠ABE=∠DAE，故③正确；
④如图，过E作EG⊥BC于G点，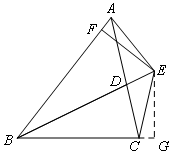

∵E是BD上的点，
∴EF=EG，
在Rt△BEG和Rt△BEF中，
，
∴Rt△BEG≌Rt△BEF（HL），
∴BG=BF，
在Rt△CEG和Rt△AEF中，
，
∴Rt△CEG≌Rt△AEF（HL），
∴AF=CG，
∴BA+BC=BF+FA+BG-CG=BF+BG=2BF，
故④正确．
故选：D．

略