如图，在平面直角坐标系xOy中，有一个等腰Rt△AOB，∠OAB=90°，直角边AO在x轴上，且AO=1，将Rt△AOB绕点O顺时针旋转90°并将两直角边延长，得到等腰Rt△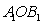，且使，再将Rt△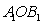绕点O顺时针旋转90°，并将两直角边延长，得到等腰Rt△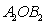，且使，…，依此规律，得到等腰Rt△，则点的坐标为(    )

• A.
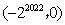
• B.
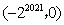
• C.
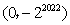
• D.

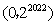
答案

正确答案：A

知识点：规律探究  

∵△AOB是等腰直角三角形，OA=1，
∴AB=OA=1，
∴A(1，0)，
将Rt△绕点O顺时针旋转90°，并将两直角边延长，得到等腰Rt△，且使，…，依此规律，
∴每4次循环一周，(0，-2)，(-4，0)，(0，8)，(16，0)，
∵2022÷4=505•••2，
∴点与在x轴的负半轴上，
∵，，，
∴点．
故答案为．
故选：A．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>