如图，在Rt△ABC中，∠ACB=90°．按以下步骤作图：①以点C为圆心、适当长为半径画弧，分别交AC，CB于点M，N；②分别以点M和点N为圆心，大于MN的长为半径画弧，两弧在∠ACB内交于点G；③作射线CG，若AC=4，D为AC边的中点，E为射线CG上一动点，则AE+DE的最小值为(    )

• A.3
• B.
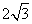
• C.
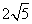
• D.5

答案

正确答案：C

知识点：勾股定理  

由题意得，CG为∠ACB的角平分线，
在CB上截取=CA，如图所示，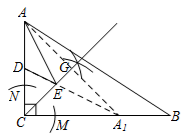

∵∠ACB=90°，
∴△是等腰直角三角形，
∴CG⊥，AG=，即CG垂直平分，
∴为点A关于CG的对称点，AE=，
∴AE+DE=+DE，
当，E，D，三点共线时AE+DE最小，
∵D为AC边的中点，AC=4，
∴=4，CD=2，
∴，
即AE+DE的最小值为，
故选：C．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>