如图,在Rt△ACB和Rt△DCE中,AC=BC=2,CD=CE,
∠CBD=15°,连接AE,BD交于点F,则BF的长为( )

- A.
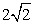
- B.
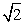
- C.
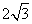
- D.
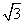
答案
正确答案:B
知识点:勾股定理
∵∠ACB=90°,∠DCE=90°,
∴∠ACB+∠BCE=∠DCE+∠BCE,
∴∠ACE=∠BCD,
∵AC=BC,CD=CE,
∴△ACE≌△BCD,
∴∠CAE=∠CBD=15°
∵在Rt△ACB中,AB=AC,
∴∠ABC=∠BAC=45°,
∴∠ABF=∠ABC+∠CBD=60°,∠BAF=∠BAC-∠CAE=30°,
∴∠AFB=180°-∠ABF-∠BAF=90°,BF=![]() AB,
AB,
∵AC=BC=2,
∴在Rt△ACB中,由勾股定理得:![]() ,
,
∴BF=![]() ,
,
故选:B.
略





