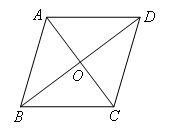
如图,四边形ABCD的对角线相交于点O,且点O是BD的中点,若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为( )
- A.40
- B.24
- C.20
- D.15
答案
正确答案:B
∵∠ABD=∠CDB,
∴AB∥CD,
∵AB=AD,点O是BD的中点,
∴∠ABD=∠ADB,AO⊥BD,
∴∠AOD=∠COD=90°,
又∵∠ABD=∠CDB,
∴∠ADB=∠CDB,
∴∠DAO=∠DCO,
∴AD=CD,
∴AB=CD,
∴四边形ABCD为平行四边形,
又∵AB=AD,
∴平行四边形ABCD为菱形,
∴![]() .
.
在Rt△AOB中,∠AOB=90°,AB=5,BO=4,
由勾股定理得,AO=3,
∴AC=6,
∴![]() .
.
略





