如图,正方形ABCD中,AB=6,G是BC的中点,将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是( )

- A.1
- B.
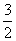
- C.2
- D.
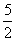
答案
正确答案:C
知识点:正方形的性质
如图,连接AE.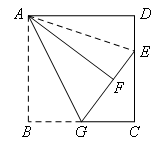
∵四边形ABCD为正方形,△ABG沿AG对折至△AFG
∴AF=AB=AD,∠AFG=∠B=∠D=90°
∴∠AFE=∠D=90°
∵AE=AE
∴Rt△AFE≌Rt△ADE(HL)
∵G是BC的中点,BC=6,若设DE=x
则CG=3,FG=BG=3,EF=DE=x,CE=6-x
Rt△CGE中,由勾股定理CG2+CE2=EG2
即32+(6-x)2=(3+x)2,解得x=2
∴DE的长是2
略





