如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BH⊥AE,垂足为点H,延长BH交CD于点F,连接AF.若正方形边长是5,BE=2,则AF的长为( )

- A.4
- B.
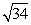
- C.
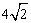
- D.
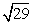
答案
正确答案:B
知识点:正方形的性质
∵四边形ABCD为正方形
∴AB=BC,∠ABC=∠C=90°
∵BH⊥AE
∴∠BAE+∠BEA=90°,∠EBH+∠BEA=90°
∴∠BAE=∠EBH
∴△ABE≌△BCF(ASA)
∴CF=BE
∵BC=5,BE=2
∴AD=5,DF=3
则Rt△ADF中,利用勾股定理可得AF=![]()
略





