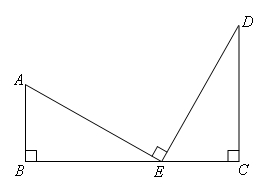
如图，树AB与树CD之间相距13m，小华从点B沿BC走向点C，行走一段时间后他到达点E，此时他仰望两棵大树的顶点A和D，且两条视线的夹角正好为90°，EA=ED，已知大树AB的高为5m，小华行走的速度为1m/s，求小华行走到点E的时间．

由题意知∠B=∠C=∠AED=90°，所以∠AEB+∠DEC=90°，∠DEC+∠D=90°，所以∠AEB=∠D；又有EA=ED，观察这三组条件在图中的位置，可根据判定定理AAS，得△ABE≌△ECD．
全等三角形对应边相等，可得EC=AB=5，又有BC=13，所以BE=BC-EC=13-5=8，所以小华行走到点E的时间是8÷1=8（s）．
故选C．

略