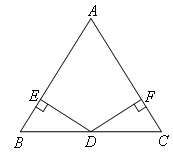
如图，在△ABC中，点D是边BC的中点，DE⊥AB于点E，DF⊥AC于点F，BE=CF．求证：△ABC是等腰三角形．

证明：如图
∵点D是边BC的中点，
∴
∵DE⊥AC，DF⊥AB，
∴
在Rt△BDE和Rt△CDF中，

∴Rt△BDE≌Rt△CDF（HL），
∴
∴△ABC是等腰三角形．
①∠BED=∠CFD=90°；②BD＝CD；③∠B＝∠C；④．
以上空缺处依次填写最恰当的是(    )

答案

正确答案：B

知识点：略

证明：如图，
∵D是BC的中点，
∴BD＝CD，
∵DE⊥AC，DF⊥AB，
∴∠BFD=∠DEC=90°
在Rt△BDE和Rt△CDF中，

∴Rt△BDE≌Rt△CDF（HL）．
∴∠B＝∠C
∴△ABC是等腰三角形．
故选B

略

下载次数：0