（1）如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°.
小颖把△ABE绕点A逆时针旋转90°至△ADG，从而发现EF=BE+FD，请你利用图1证明上述结论．
（2）如图2，四边形ABCD中，∠BAD≠90°，AB=AD，∠B+∠ADC=180°，
点E、F分别在边BC、CD上，试探究：当∠EAF与∠BAD满足何种关系时，
仍有EF=BE+FD，并证明你的结论；
（3）如图3，四边形ABCD中，AB=AD=80，∠B=60°，∠ADC=120°，∠BAD=150°，点E、F分别在边
BC、CD上，且AE⊥AD，DF=），连接EF，求EF的长（结果保留根号）．

（2）中∠EAF与∠BAD应满足的关系是(    )

• A.∠EAF=∠BAD
• B.∠EAF=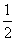∠BAD
• C.∠EAF=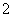∠BAD
• D.∠EAF+∠BAD=180°

答案

正确答案：B

知识点：旋转的性质  类比探究问题  

见第4题中解析

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>