图1的长方形ABCD中，点E在AD边上，AD∥BC，∠A=∠D=90°，∠BEA=60°．现分别以
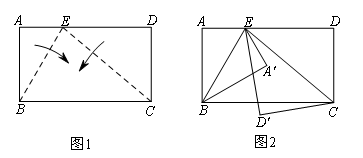
BE，CE为折线，将A，D向BC的方向折过去，图2为对折后A，B，C，D，E五点在同一平面上的位置图．若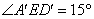，则∠BCE的度数为(    )

分别以BE，CE为折线，将A，D向BC的方向翻折，
则直线BE，CE分别是对称轴，
根据轴对称的性质可知∠BEA′=∠BEA=60°，
∠DEC=∠D′EC=∠D′ED，
结合∠A′ED′=15°，可以得到∠BED′=∠BEA′-∠A′ED′=45°，
因此∠AED′的度数为105°，进而得到∠D′ED的度数为75°，
所以∠DEC=37.5°，由AD∥BC可得∠BCE=∠DEC=37.5°．
故选D．

略