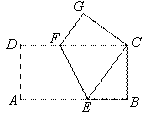
如图，将矩形纸片ABCD沿EF折叠，使点A与点C重合，点D落在点G处，EF为折痕，AB=8，AD=4，则四边形ECGF的面积为（）
- A.6
- B.10
- C.12
- D.16
答案
正确答案：D
知识点：勾股定理的应用
因为将矩形纸片ABCD沿EF折叠，使点A与点C重合，点D落在点G处，EF为折痕，所以CE=AE，DF=FG，AD=CG=4，∠AEF=∠CEF，又因为∠CFE=∠FEA，所以CF=CE，在直角△CEB中，设AE=CE=x，则BE=8-x，根据勾股定理得，
，解得x=5，即CE=CF=5，DF=FG=3，梯形ECGF的面积就是（3+5）×4÷2=16
略
WORD格式（
