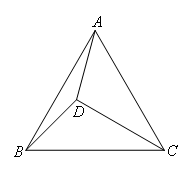
如图,点D是等边三角形ABC内部一点,AD=BD=1,CD=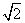 ,则∠ADC=( )
,则∠ADC=( )
- A.105°
- B.115°
- C.135°
- D.150°
答案
正确答案:A
观察图形,含有等腰结构;
将线段CD绕点C顺时针旋转60°至CD′,连接AD′,DD′.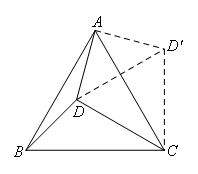
∵CD=CD′,∠DCD′=60°
∴△DCD′是等边三角形,且∠CDD′=60°
∴DD′=CD=![]()
∵∠ACB=60°
∴∠BCD=∠D′CA
∵BC=AC
∴△BCD≌△ACD′(SAS)
∴AD′=BD=1
在△ADD′中,AD=1,AD′=1,DD′=![]()
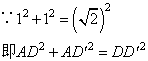
∴△ADD′是等腰直角三角形,且∠DAD′=90°
∴∠ADD′=45°
∴∠ADC=45°+60°=105°
故选A.
略








