如图，已知AC平分∠DAB，CE⊥AB于点E，AB=AD+2BE，则下列结论：
①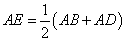；②∠ADC+∠B=180°；③CD=CB；④．
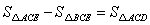其中正确的有(    )

如图，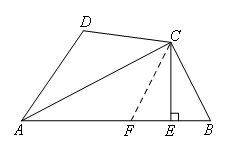

①在EA上截取EF=BE，连接CF．
∵AB=AD+2BE=AF+EF+BE，EF=BE
∴AB=AD+2BE=AF+2BE
∴AD=AF
∴AB+AD=AF+EF+BE+AD=2AF+2EF=2(AF+EF)=2AE
∴
因此①正确．
②由①知，AD=AF
∵AC平分∠DAB
∴
在△ACD与△ACF中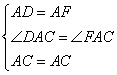

∴△ACD≌△ACF（SAS）
∴∠ADC=∠AFC
∵CE垂直平分BF
∴CF=CB
∴∠CFB=∠B
又∵∠AFC+∠CFB=180°
∴∠ADC+∠B=180°
因此②正确．
③由②知，△ACD≌△ACF
∴CD=CF
又∵CF=CB
∴CD=CB
因此③正确．
④易证△BCE≌△FCE
∴
又∵△ACD≌△ACF
∴
∴
因此④正确．
故选D．

略