已知：如图，直线AB∥CD，EF分别交AB，CD于点G，M，射线GH，MN分别
平分∠BGM，∠DMF．
求证：GH∥MN．

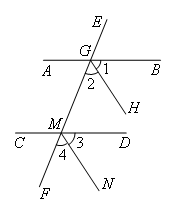
证明：如图，

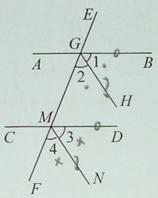
∵AB∥CD（已知）
∴∠BGM=∠DMF（                  ）
∵GH平分∠BGM（已知）
∴（角平分线的定义）
∵MN平分∠DMF（已知）
∴（角平分线的定义）
∴            （等式性质）
∴GH∥MN（                  ）
①∠2=∠4；②∠1=∠3；③两直线平行，同位角相等；④等量代换；⑤同位角相等，两直线平行；
⑥同旁内角互补，两直线平行；⑦内错角相等，两直线平行．
以上空缺处依次所填正确的是(    )

• A.③②⑦
• B.④②⑤
• C.③①⑤
• D.③①⑦

答案

正确答案：C

知识点：平行线的判定  平行线的性质  角平分线  

要证GH∥MN，考虑同位角，内错角，同旁内角，
本题利用同位角相等，两直线平行较为简单．
先从已知条件AB∥CD入手，利用两直线平行，同位角相等，得∠BGM=∠DMF（因此第一个空选③）．
再利用角平分线的定义，得，，
利用等式性质得，∠2=∠4（因此第二个空选①）．
由同位角∠2=∠4，利用同位角相等，两直线平行，得GH∥MN（因此第三个空选⑤）．
故选C．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>