如图，已知抛物线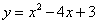与x轴交于两点A、B，其顶点为C．
(1)对于任意实数m，点M（m，-2）是否在该抛物线上?请说明理由；
(2)求证:△ABC是等腰直角三角形；
(3)已知点D在x轴上，那么在抛物线上是否存在点P，使得以B、C、D、P为顶点的四边形是平行四边形？若存在，求点P的坐标；若不存在，请说明理由．

（1）假如点M（m，-2）在该抛物线上，则-2=m²-4m+3，m²-4m+5=0，由于△=（-4）²-4×1×5=-4＜0，此方程无实数解，所以点M（m，-2）不会在该抛物线上；
（2）当y=0时，x²-4x+3=0，x₁=1，x₂=3，由于点A在点B左侧，
∴A(1，0)，B(3，0)y=x²-4x+3=(x-2)²-1，
∴顶点C的坐标是（2，-1），
由勾股定理得，AC=，BC=，AB=2，
∵AC²+BC²=AB²，
∴△ABC是等腰直角三角形；
(3)存在这样的点P．

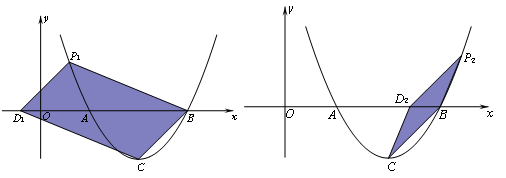
根据对角线互相平分的四边形是平行四边形，因此连接点P与点C的线段应被x轴平分，
∴点P的纵坐标是1，
∵点P在抛物线y=x²-4x+3上，
∴当y=1时，即x²-4x+3=1，解得x₁=2-，x₂=2+，
∴点P的坐标是（2-，1）或（2+，1）．

略