如图,已知反比例函数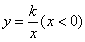 的图象经过点
的图象经过点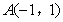 ,过点A作AB⊥y轴,垂足为点B,在y轴的正半轴上取一点
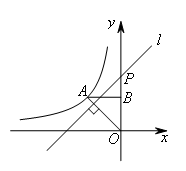
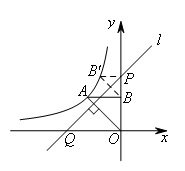
,过点A作AB⊥y轴,垂足为点B,在y轴的正半轴上取一点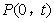 ,过点P作直线OA的垂线l,以直线l为对称轴,若点B经过轴对称变换后,得到的点B′在此反比例函数的图象上,则t的值为( )
,过点P作直线OA的垂线l,以直线l为对称轴,若点B经过轴对称变换后,得到的点B′在此反比例函数的图象上,则t的值为( )
- A.
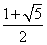
- B.
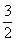
- C.
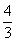
- D.
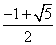
答案
正确答案:A
如图,作点B关于直线l的对称点![]() ,连接
,连接![]() ,
,
∵![]() ,
,
∴反比例函数为![]() .
.
由题意,![]() ⊥l,OA⊥l,
⊥l,OA⊥l,
∴![]() ∥OA,
∥OA,
∴∠AOB=∠![]() =45°,
=45°,![]() ,
,
∴∠![]() =45°.
=45°.
∵点B关于直线l对称的点是![]() ,
,
∴![]() ,
,
∴∠![]() =∠
=∠![]() =45°,
=45°,
∴∠![]() =90°,即
=90°,即![]() ⊥y轴,
⊥y轴,
∴△![]() 是等腰直角三角形.
是等腰直角三角形.
∵![]() ,t>0,
,t>0,
∴![]() ,
,
∴![]() ,
,
∵![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,
∴![]() ,整理得
,整理得![]() ,
,
解得![]() ,
,
∴![]() .
.
略








