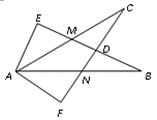
如图所示,∠E=∠F=90°，∠B=∠C，AE=AF，结论：①EM=FN；②CD=DN；③∠FAN=∠EAM；④△ACN≌△ABM ．其中正确的有（     ）个

由已知条件易证△ABE≌△ACF（AAS），得∠BAE=∠CAF，AB=AC，BE=CF。
对于①，∠EAM=∠BAE-∠BAM,∠FAN=∠CAF-∠CAB，所以∠EAM=∠FAN，在△AEM和△AFN中，∠E=∠F=90°，AE=AF，∠EAM=∠FAN，所以△AEM≌△AFN（ASA），得EM=FN，故①正确；
对于②，由△AEM≌△AFN得AM=AN，又AC=AB，所以CM=AC-AM=AB-AN=BN，从而易证△CDM≌△BDN，得CD=BD，若②正确，即CD=DN，则BD=DN，即△BDN为等腰三角形，∠DNB=∠B，又∠DNB=∠NAC+∠C，∠B=∠C，推出矛盾，所以②不正确；
对于③，由△AEM≌△AFN，得∠EAM=∠FAN，故③正确；
对于④，在△ACN和△ABM中，∠CAN=∠BAM,AC=AB,∠C=∠B，得△CAN≌△BAM（ASA），故④正确。
综上，①③④正确，正确个数为3个，答案为C。

略