如图所示，（1）正方形ABCD及等腰Rt△AEF有公共顶点A,∠EAF=90°,连接BE、DF.将Rt△AEF绕点A旋转,在旋转过程中，BE、DF具有怎样的数量关系和位置关系？结合图(1)给予证明；(2)将（1）中的正方形ABCD变为矩形ABCD，等腰Rt△AEF变为Rt△AEF，且AD=kAB,AF=kAE,其他条件不变.(1)中的结论是否发生变化？结合图(2)说明理由；(3)将（2）中的矩形ABCD变为平行四边形ABCD，将Rt△AEF变为△AEF，且∠BAD=∠EAF=
，其他条件不变.(2)中的结论是否发生变化？结合图(3)，如果不变，直接写出结论；如果变化，直接用k表示出线段BE、DF的数量关系，用表示出直线BE、DF形成的锐角
.
答案
（1）证明：延长DF分别交AB、BE于点P、G.
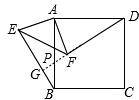
在正方形ABCD和等腰直角△AEF中
AD=AB,AF=AE,
∠BAD=∠EAF=90°
∴∠FAD=∠EAB
∴△FAD≌△EAB
∴∠AFD=∠AEB，DF=BE
∵∠AFD+∠AFG=180°，
∴∠AEB+∠AFG=180°，
∵∠EAF=90°，
∴∠EGF=180°-90°=90°，
∴DF⊥BE
（2）数量关系改变，位置关系不变.DF=kBE，DF⊥BE.延长DF交EB于点H，
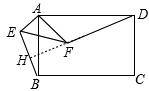
∵AD=kAB，AF=kAE
∴
，
∴
∵∠BAD=∠EAF=90°
∴∠FAD=∠EAB
∴△FAD∽△EAB
∴
∴DF=kBE∵△FAD∽△EAB，
∴∠AFD=∠AEB，
∵∠AFD+∠AFH=180°，
∴∠AEH+∠AFH=180°，
∵∠EAF=90°，
∴∠EHF=180°-90°=90°，
∴DF⊥BE
(3)不改变．DF=kBE，β=180°-α延长DF交EB的延长线于点H
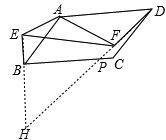
∵AD=kAB,AF=kAE
∴
=k,
=k
∴=
∵∠BAD=∠EAF=
∴∠FAD=∠EAB
∴△FAD∽△EAB
∴
==k
∴DF=kBE由△FAD∽△EAB得∠AFD=∠AEB
∵∠AFD+∠AFH=180
∴∠AEB+∠AFH=180°
∵四边形AEHF的内角和为360°，
∴∠EAF+∠EHF=180°
∵∠EAF=,∠EHF=
∴+=180°
∴=180°-
知识点：全等三角形的判定与性质 多边形内角与外角 相似三角形的判定与性质
（1）根据旋转的过程中线段的长度不变，得到AF=AE，又∠BAE与∠DAF都与∠BAF互余，所以∠BAE=∠DAF，所以△FAD≌△EAB，因此BE与DF相等，延长DF交BE于G，根据全等三角形的对应角相等和四边形的内角和等于360°求出∠EGF=90°，所以DF⊥BE；
（2）等同（1）的方法，因为矩形的邻边不相等，但根据题意，可以得到对应边成比例，所以△FAD∽△EAB，所以DF=kBE，同理，根据相似三角形的对应角相等和四边形的内角和等于360°求出∠EHF=90°，所以DF⊥BE；（3）与（2）的证明方法相同，但根据相似三角形的对应角相等和四边形的内角和等于360°求出∠EAF+∠EHF=180°，所以DF与BE的夹角β=180°-α．
略
WORD格式（
