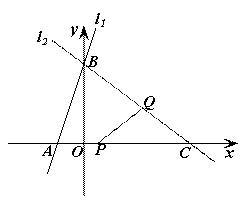
如图，已知直线l₁的解析式为y=3x+6，直线l₁与x轴、y轴分别相交于A、B两点，直线l₂经过B、C两点，点C的坐标为（8，0），又已知点P在x轴上从点A向点C移动，点Q在直线l₂从点C向点B移动．点P、Q同时出发，且移动的速度都为每秒1个单位长度，设移动时间为t秒（1＜t＜10）．（1）求直线l₂的解析式．（2）设△PCQ的面积为S，请求出S关于t的函数关系式．（3）试探究：当t为何值时，△PCQ为等腰三角形？

（1）由题意，知B(0，6)，C(8，0).
设直线l₂的解析式为y=kx+b，则，解得，b=6．
∴l₂的解析式为．
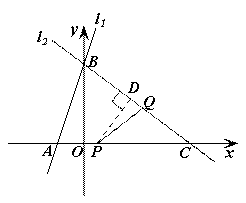
（2）解法一：如图，过P作PD⊥l₂于D，则△PDC∽△BOC．

∴．
由题意知，OA=2，OB=6，OC=8，
∴，PC=10－t
∴，∴
∴
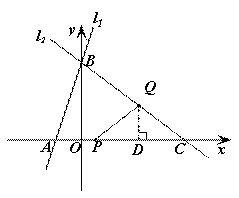
解法二：如图，过Q作QD⊥x轴于D，则△CQD∽△CBO．

∴．
由题意知，OA=2，OB=6，OC=8．
∴，
∴，．

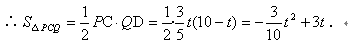
（3）根据等腰三角形的基本特征画出图形，进行分类讨论，再表达出相对应的个线段的长度建立等式来进行求解．要想使△PCQ为等腰三角形，需满足CP=CQ，或QC=QP，或PC=PQ．
①当CP=CQ时（如图①），得10－t=t，解得t=5．

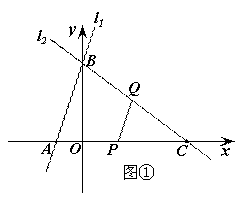
②当QC=QP时（如图②），

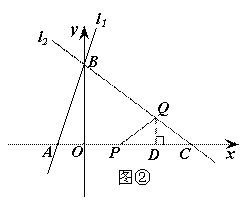
过Q作QD⊥x轴于D，则．
∵△QDC∽△BOC，∴，
即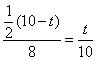，解得．
③当PC=PQ时（如图③），

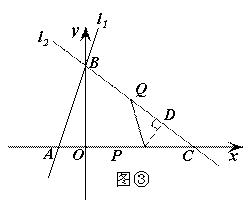
过P作PD⊥l₂于D，则
∵△CDP∽△COB，∴．
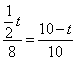∴，解得．
综上所述，当t=5，或，或时，△PCQ为等腰三角形．

略