在Rt△ABC中,∠BAC=90°,AB=AC=2,以AC为一边,在△ABC外部作等腰Rt△ACD,则线段BD的长为( )
- A.
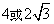
- B.

- C.
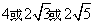
- D.
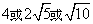
答案
正确答案:D
1.解题要点
①首先画出基本图形等腰直角△ABC;
②△ACD中,点A,C是定点,要作出等腰直角三角形,需要进行分类讨论,
分别以A,C,D轮流作为直角顶点,画出符合题意的图形;
④根据对应的图形,有序操作,求解,验证.
2.解题过程
①若∠CAD=90°且AC=AD,如图所示,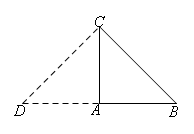
此时AD=AC=AB=2,
∴BD=AB+AD=2+2=4.
②若∠ACD=90°且CA=CD,如图所示,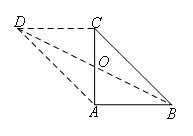
四边形ABCD是平行四边形,
∴![]() .
.
在Rt△ODC中,![]() ,
,
∴![]() .
.
③若∠ADC=90°且DC=DA,如图所示,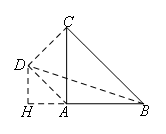
在Rt△DAC中,AC=2,∠DCA=45°,
∴![]() .
.
在Rt△DAH中,![]() ,∠DAH=45°,
,∠DAH=45°,
∴![]() ,
,
∴BH=BA+AH=2+1=3,
在Rt△BDH中,![]() .
.
∴BD的长可能为![]() .
.
故选D.
略







