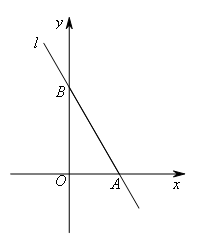
如图，在平面直角坐标系中，直线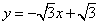与x轴、y轴分别交于A，B两点，
点P是y轴上一动点，则在坐标平面内是否存在点Q，使得以A，B，P，Q为顶点的四边形是菱形？
（1）处理这样的问题，我们一般是转化为等腰三角形的存在性问题，那此题我们转化为哪个等腰三角形的存在性问题？(    )

• A.△ABQ
• B.△ABP
• C.△APQ
• D.△BPQ

答案

正确答案：B

知识点：菱形的存在性（转等腰）  

①先分析定点、动点
定点：A，B
动点：P，Q
②连接AB成为定线段，当AB为菱形的边时，如图

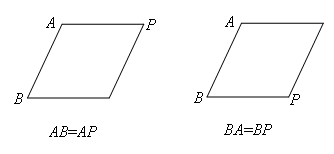
当AB为菱形的对角线时，如图

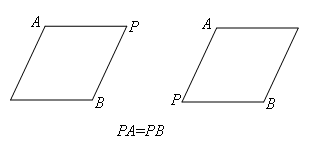
综上，可转化为等腰△ABP的存在性，然后通过作两条平行线（或沿等腰三角形底边翻折）找到点Q.

略

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>