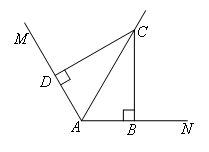
如图1,已知∠MAN=120°,AC平分∠MAN,∠ABC=∠ADC=90°,可以证明:①DC=BC;②AC=AB+AD.
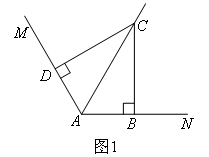
(1)如图2,把题干中的条件“∠ABC=∠ADC=90°”改为“∠ABC+∠ADC=180°”,其他条件不变,要证明题干中的两个结论成立,下列辅助线不合适的是( )
- A.
- B.
- C.
- D.
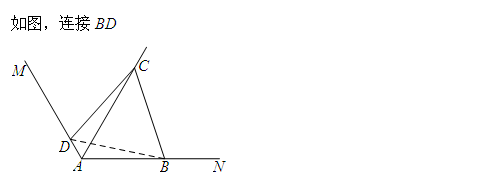
答案
正确答案:D
知识点:中考数学几何中的类比探究
1.解题要点
①弄清题干中结论是如何证明的,利用含30°角的直角三角形,得到![]() ,进而证明结论.
,进而证明结论.
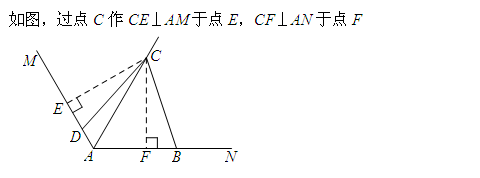
②要证明线段之间的关系,可以用截长补短的方法.或者照搬题干中的图形,补全来做:过点C作CE⊥AM于点E,CF⊥AN于点F,思路能够进行下去,路线图如下,
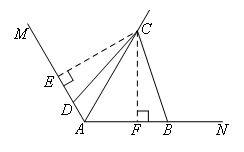
第一步:辅助线,过点C作CE⊥AM于点E,CF⊥AN于点F.
第二步:由题干可知AC=AE+AF.
第三步:△CED≌△CFB(AAS),DE=BF.
第四步:AC=AF+DE+AD=AF+BF+AD=AB+AD.
不变特征是:∠MAN=120°,AC平分∠MAN,同时∠ABC+∠ADC=180°.
2.解题过程
下面分别说明A,B,C选项中给出的证明思路的合理性,用路线图的方式来说明,完整过程请自行写出.
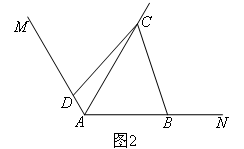
A选项:补短思想.
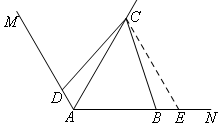
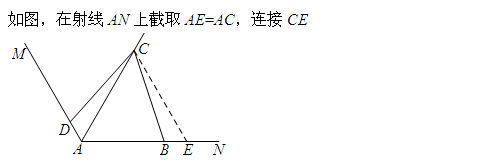
第一步:辅助线,在射线AN上截取AE=AC,连接CE.
第二步,△ACE为等边三角形.
第三步:△CDA≌△CBE(AAS).
第四步:AC=AE=AB+BE=AB+AD.
B选项:类比构造思想,补成与题干类似的图形,路线图见上面的解题要点.

C选项:利用角平分线的对称思想.
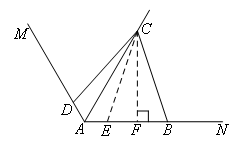
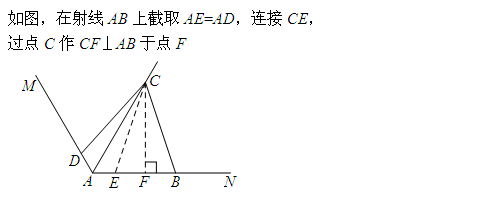
第一步:辅助线,在射线AB上截取AE=AD,连接CE,过点C作CF⊥AB于点F.
第二步:△CDA≌△CEA(SAS),∠ADC=∠AEC,∠CEF=∠CBF.
第三步:CE=CB,EF=BF.
第四步:AC=2AF=AB+AD.
只有D选项中的思路证明不了题干中的两个结论.
略









