如图1,已知正方形ABCD和正方形QMNP,M是正方形ABCD的对称中心,MN交AB于点F,QM交AD于点E,易证ME=MF.
(1)如图2,若将题干中的“正方形”改为“矩形”,且AB:BC=1:2,其他条件不变,则ME和MF之间的数量关系为( )
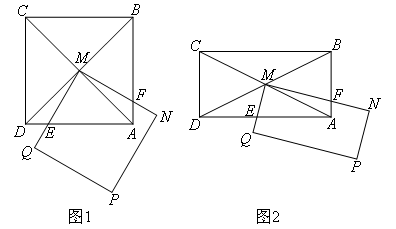
- A.
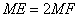
- B.
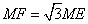
- C.
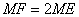
- D.
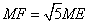
答案
正确答案:C
知识点:中考数学几何中的类比探究
1.解题要点
①图1中,要证两条线段相等,可以放在两个三角形中证全等.
由于∠MEA=∠MFB(利用四边形内角和得到),结合∠EMF是斜直角,
自然过点M分别作MG⊥AB于点G,MH⊥AD于点H,
通过证明△MHE≌△MGF,得到结论.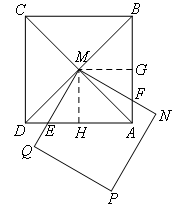
②图2中,“∠BAD=∠QMN=90°”产生的“∠MEA=∠MFB”没有发生变化,
所以照搬上面分析的辅助线:过点M分别作MG⊥AB于点G,MH⊥AD于点H.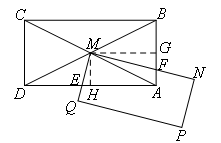
可以证明△MHE∽△MGF,从而![]() ,
,
由于![]() ,可得
,可得![]() .
.
2.解题过程
如图,过点M分别作MG⊥AB于点G,MH⊥AD于点H.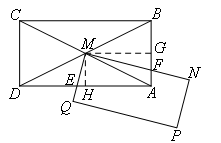
则四边形MHAG是矩形,
∴∠MHE=∠MGF=90°,MG=AH.
∵∠EMF+∠EAF=180°,
∴∠MEH+∠MFA=180°,
∴∠MEH=∠MFG,
∴△MEH∽△MFG,
∴![]() .
.
∵△MHA∽△CDA,
∴![]() ,
,
∴![]() ,即MF=2ME.
,即MF=2ME.
略








