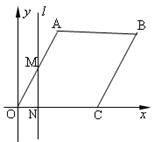
如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC= 60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒(0≤t≤4),则能大致反映S与t的函数关系的图象是( )
秒(0≤t≤4),则能大致反映S与t的函数关系的图象是( )
- A.
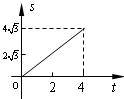
- B.

- C.

- D.
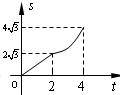
答案
正确答案:C
知识点:运动变化型问题
解:法一(直接法):过A作AH⊥x轴于H,∵OA=OC=4,∠AOC=60°,∴OH=2,由勾股定理得:AH=![]() ,
,
①当0≤t<2时,ON=t,MN=![]() t,S=
t,S=![]() ON•MN=
ON•MN=![]() ;
;
②当2<t≤4时,ON=t,S=![]() ON•
ON•![]() =
=![]() t.
t.
故选C.法二(技巧法):根据两变量积的图象的变化规律:同增同减,开口向上,一增一减,开口向下。
当0≤t<2时,两变量同增,图象是二次函数,开口向上,排除A、D,
当2<t≤4时,一个变量不变,一个变量增加,图象是一次函数,斜率为正,故选C.
略








