已知：如图，在△ABC中，点D是BC的中点，DF⊥AB于F，DE⊥AC于E，DF=DE．
求证：AB=AC．

证明：如图，
∵点D是BC的中点
∴BD=CD
∵DF⊥AB，DE⊥AC
∴∠BFD=∠AFD=∠AED=∠CED=90°
在Rt△BDF和Rt△CDE中
                           
∴Rt△BDF≌Rt△CDE（     ）
∴BF=CE
在Rt△AFD和Rt△AED中
                           
∴Rt△AFD≌Rt△AED（HL）
∴AF=AE
∴BF+AF=CE+AE
即AB=AC
请你仔细观察下列序号所代表的内容：
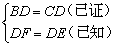①；②；③SAS；④HL；

⑤；⑥．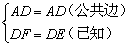
以上空缺处依次所填正确的是(    )

• A.①③⑤
• B.②④⑥
• C.②④⑤
• D.①③⑥

答案

正确答案：B

知识点：全等三角形证明过程训练  全等三角形的性质和判定  

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>