如图,在四边形ABCD中,对角线AC,BD交于点O,已知AC=BD,M,N分别是AD,BC的中点,MN与AC,BD分别交于点E,F,则△OEF是( )
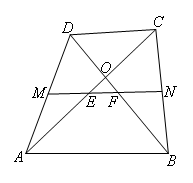
- A.等边三角形
- B.等腰三角形
- C.直角三角形
- D.等腰直角三角形
答案
正确答案:B
知识点:中位线
如图,取CD的中点G,连接MG,NG.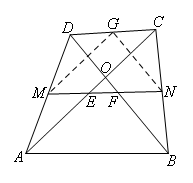
∵M,G分别是AD,CD的中点,
∴MG是△ACD的中位线,
∴MG∥AC,![]() ,
,
同理可证:NG∥BD,![]() ,
,
∵AC=BD,
∴MG=NG,
∴∠GMN=∠GNM,
∵∠GMN=∠OEF,∠GNM=∠OFE,
∴∠OEF=∠OFE,
∴△OEF是等腰三角形,
∵题干中没有涉及到有特殊的角度存在,
∴不能证明△OEF三边相等或者∠EOF为直角,
综上:△OEF是等腰三角形.
故选B
略








