已知在Rt△ABC中,∠C=90°,AC=6,BC=8,将它的一个锐角翻折,使该锐角顶点落在其对边的中点D处,折痕交另一直角边于点E,交斜边于点F,则tan∠CDE的值为 .
- A.
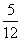
- B.
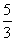
- C.
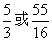
- D.
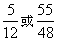
答案
正确答案:D
知识点:翻折变换(折叠问题)
1.解题要点
①标注条件(直角和直角边长).
②直角三角形有两个锐角,需要分类讨论,翻折∠A或翻折∠B.
③根据题意画出图形,找到∠CDE,先看翻折锐角∠A的情况.
取BC的中点D,连接AD,作AD的垂直平分线,交AC于点E,交AB于点F,连接DE.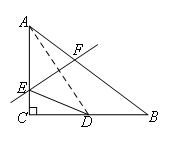
在Rt△CDE中求tan∠CDE,即CE和CD的比值,CD已知,问题转化为求CE的长.
利用折叠转移条件,在Rt△CDE中利用勾股定理求CE的长,进而求出tan∠CDE的值.
④翻折∠B,处理思路和翻折∠A一致.
2.解题过程
①如图,翻折∠A.
∵D是BC的中点,
∴CD=4.
设CE=x,则AE=6-x,
由折叠得,DE=AE=6-x.
在Rt△CDE中,由勾股定理得,![]() ,
,
解得![]() ,
,
∴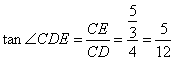 .
.
②如图,翻折∠B.
∵D是AB的中点,
∴CD=3.
设CE=x,则BE=8-x,
由折叠得,DE=BE=8-x.
在Rt△CDE中,由勾股定理得,![]() ,
,
解得![]() ,
,
∴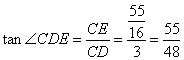 .
.
综上得,tan∠CDE的值为![]() .
.
略







