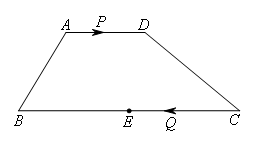
如图,在梯形ABCD中,AD∥BC,AD=5,BC=14,E是BC的中点.点P以每秒2个单位长度的速度从点A出发,沿AD向点D运动;点Q以每秒4个单位长度的速度从点C同时出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.设运动时间为t秒,则当t的值为( )时,以P,Q,E,D为顶点的四边形是平行四边形.
- A.1
- B.
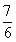
- C.

- D.1或2
答案
正确答案:D
知识点:动点问题
1.解题要点
①研究基本图形,将信息进行标注.
②分析运动状态,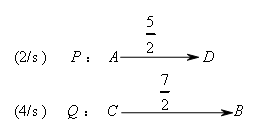
研究起点,终点,确定时间范围,
由线段图可知![]() .
.
③以P,Q,E,D为顶点的四边形中,PD∥QE,若四边形是平行四边形,只需保证PD=EQ.
④由于点Q可在点E的左侧或右侧,所以需要进行分类讨论.
⑤在每一时间段上进行求解,验证.
2.解题过程
由题意得,AP=2t,PD=5-2t,CQ=4t,CE=7.
①当点Q在线段CE上,四边形PEQD是平行四边形时,
PD=EQ,![]() ,如图所示,
,如图所示,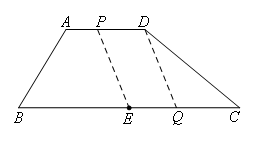
∵![]() ,
,
∴![]() ,解得
,解得![]() ,符合题意.
,符合题意.
②当点Q在线段BE上,四边形PQED是平行四边形时,
PD=QE,![]() ,如图所示,
,如图所示,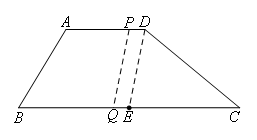
∵![]() ,
,
∴![]() ,解得
,解得![]() ,符合题意.
,符合题意.
综上可得,当t的值为1或2时,以P,Q,E,D为顶点的四边形是平行四边形.
略








