如图，在矩形ABCD中，AB=1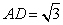，，AF平分∠DAB，过点C作CE⊥BD于E，
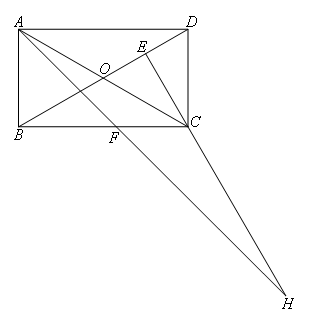
延长AF，EC交于点H，有下列结论：①AF=FH；②BO=BF；③CA=CH；④BE=3ED．其中正确的是(    )

在矩形ABCD中，
∵AB=1，，
∴BD=AC=2，
OB=OA=OD=OC=1．
∴OB=OA=OD=OC=AB=CD=1，
∴△OAB，△OCD为等边三角形．
∵AF平分∠DAB，
∴∠FAB=45°，即△ABF为等腰直角三角形．
∴BF=AB=1，BO=BF，②正确；
∴∠CAH=15°．
∵CE⊥BD
∴∠OCE=30°，，
∴∠AHC=15°，
∴CA=CH，③正确；
∴BE=3ED．④正确；
AF=FH无法证明，故①错误。
故选D．

略