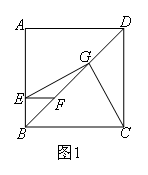
（1）如图1，在正方形ABCD的边AB上任取一点E，过点E作EF⊥AB，交BD于点F，取DF的中点G，连接EG，CG．为了研究线段EG和CG之间的数量和位置关系，可通过作辅助线：延长EG，交AD的延长线于点H，连接EC，HC，来进行分析．则得到的结论是(    )

点击查看解析视频：http://v.xxt.cn/course/video.do?id=13003
1．解题要点
利用题干中给出的辅助线信息继续研究，寻找进一步的结论来说明EG和CG之间的关系．

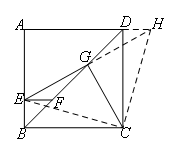
由“平行＋中点”可以得到DH=EF=BE，则△CBE≌△CDH（SAS），进而得到△ECH是等腰直角三角形，所以EG=CG且EG⊥CG．
2．解题过程
如图，延长EG，交AD的延长线于点H，连接EC，HC．


由题意得，EF∥AD，△BEF是等腰直角三角形．
∵G是DF的中点，
∴FG=DG．
∵DH∥EF，
∴∠DHG=∠FEG，∠EFG=∠HDG，
∴△EFG≌△HDG，
∴DH=EF=BE，EG=HG．
∵BC=DC，∠EBC=∠HDC=90°，
∴△CBE≌△CDH，
∴EC=HC，∠BCE=∠DCH，
∴∠ECH=∠ECD+∠DCH=∠ECD+∠BCE=90°，
∴△ECH是等腰直角三角形．
∵EG=HG，
∴EG=CG且EG⊥CG．

略