如图,已知直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕点C顺时针旋转
90°至三角板 的位置后,再沿CB方向向左平移,使点
的位置后,再沿CB方向向左平移,使点 落在原三角板ABC的斜边AB上,则三角板
落在原三角板ABC的斜边AB上,则三角板 平移的距离为( )
平移的距离为( )

- A.6cm
- B.4cm
- C.
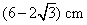
- D.
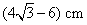
答案
正确答案:C
1.解题要点
理解题意,要求点B′平移的距离,首先要画出图形,找到平移的线段,
考虑放在直角三角形中来研究,求出AB′的长,再利用边角关系求解即可.
2.解题过程
如图,过点B′作B′D⊥AC,垂足为点D.
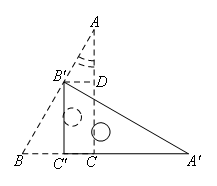
∵∠A=30°,AB=12,
∴BC=6.
由旋转可得B′C′=6,
∴![]() ,
,![]() .
.
在Rt△AB′D中,B′D=![]() ,
,
即三角板![]() 平移的距离为
平移的距离为![]() .
.
故选C.
略








