如图，AB为⊙O的直径，C为⊙O外一点，过点C作⊙O的切线，切点为B，连接AC，交⊙O于点D．若∠C=38°，点E在AB右侧的半圆上运动（不与点A，B重合），则∠AED的度数为(    )

• A.19°
• B.38°
• C.52°
• D.76°

答案

正确答案：B

知识点：圆周角定理  切线的性质  直径所对的圆周角是直角  

如图，连接BD，则∠ADB=90°，∠ABD=∠AED．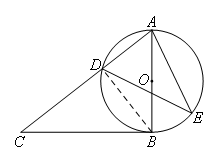

∵BC为⊙O的切线，切点为B，
∴∠ABC=90°，
∴∠C+∠CAB=∠ABD+∠CAB=90°，
∴∠C=∠ABD．
∵∠C=38°，
∴∠ABD=∠AED=38°．
故选B．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>