如图,在等腰三角形ABC中,AB=BC,∠ABC=120°,D为外角平分线上的一点,
且DC⊥BC.若BD=2,则△ABD的面积为( )
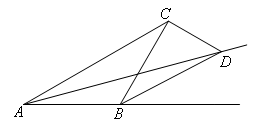
- A.1
- B.3
- C.
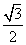
- D.
答案
正确答案:C
知识点:含30°的直角三角形
1.思路分析
①读题标注,明确目标.
本题求解三角形面积,选定计算方法,底乘高除以2,关键是明确求底和高.
②梳理信息,合理转化.
本题可视AB为底,过点D作AB的垂线作为高,进而根据30°角计算相应长度.
③结果检验.
求解三角形面积易忽略除以2,且30°角三角形三边关系需要分析清楚.
2.解题过程
如图,过点D作DE⊥AB于点E.
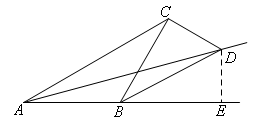
∵∠ABC=120°,
∴∠CBE=180°-120°=60°.
∵BD是△ABC的外角平分线,
∴∠CBD=![]() ×60°=30°,
×60°=30°,
∴CD=![]() BD=
BD=![]() ×2=1.……梳理信息
×2=1.……梳理信息
∵DC⊥BC,
∴BC=![]() ,
,
∴AB=BC=![]() .……合理转化
.……合理转化
∵BD是△ABC的外角平分线,DC⊥BC,
∴DE=CD=1,
∴△ABD的面积为![]() .……结果检验
.……结果检验
故选C.
略








