如图，O是正方形ABCD的对角线BD上一点，⊙O与边AB，BC都相切，点E，F分别在
边AD，DC上．现将△DEF对折，折痕EF与⊙O相切，且点D恰好落在圆心O处．若DE=2，则正方形ABCD的边长为(    )

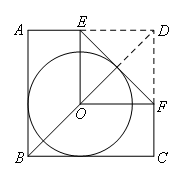
• A.3
• B.4
• C.
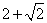
• D.

答案

正确答案：C

知识点：正方形的性质  直线与圆的位置关系  切线的性质  翻折变换(折叠问题)  

如图，延长FO交AB于点G，则点G是切点．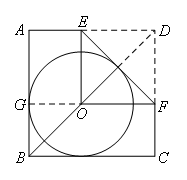

由题意得，，
∴⊙O的半径是，即，
∴．

略

下载次数：3

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>